中学校の図形分野で苦手にする人が多いのが、対頂角や同位角、錯角といった角度を求める問題です。
特に錯角を利用した問題を解けない人もいるのではないでしょうか。
対頂角や同位角、錯角については、単に角度を求める問題ばかりではなく、証明問題にも活かす場面があります。
そのため、基本事項をしっかりと身につけておくことが大事です。
今回は、対頂角や同位角、錯角について基本の解説から練習問題までご用意しました。
また、数学の学習方法についても解説していますので、ぜひ参考にしてください。

平行四辺形の対頂角

「対頂角は等しい」と明確に暗記している人も多いと思います。
しかし、なぜ「対頂角が等しいのか？」を説明できるでしょうか。
対頂角が等しい理由は明確にあります。
その理由を証明できれば、理解も深まります。

【証明】なぜ対頂角の角度は同じになるのか

対頂角が等しくなる理由は、直線が示す角度（180°）を利用すると証明できます。
例として2直線を1点で交わらせて、上下左右の角を4つ作ります。
そして、左右の角をそれぞれA、Bにしてみましょう。
ここで、上に位置する角を100°とします。
そうすると右に位置する角Aと上の角は1直線上にあるので、合計すると180°になります。
よって、角Aは80°となるのです。
同様に上に位置する角と左に位置する角Bも一直線上にあるため、角Bも80°となります。
すなわち角Aと角Bは等しくなるため、対頂角が等しいことが証明されました。
このような理由に触れることで公式や定理の理解も深まります。

同位角と錯角の関係とは

対頂角だけではなく、同位角や錯角についての理解も深めましょう。
同位角や錯角は対頂角と多少性質の異なる部分があります。
それぞれの関係を解説します。

平行線であれば、同位角・錯角のそれぞれの角度は同じ

平行線がある場合は、同位角と錯角はそれぞれ同じ角度になります。
まず2直線が平行であり、その直線に交わるような直線を1本描いたとします。
そして平行な2直線と交わった1本の直線で出来上がった角で、向きが同じ位置にある角を同位角と言います。
平行な2直線と交わる1本の直線によって、左右に角ができますが、同位角は右側同士、もしくは左側同士にある位置関係です。
2本の平行線を用意した場合は、4パターンの同位角があります。
次に平行な2直線と1本の直線で出来上がった角においては、向かいにある角が錯角の位置関係であり、角の大きさが等しくなります。
錯角も4パターンあります。
同位角も錯角も位置関係をイメージできるように図で覚えてみてください。

【証明】なぜ同位角と錯角の角度は同じになるのか

平行線において、なぜ同位角と錯角が同じ角度になるのか、それを証明していきます。
最もシンプルに結論を言うと、同位角の対頂角が錯角になるからです。
もちろん、錯角の対頂角が同位角でもあります。
もう少し詳しい証明もしていきましょう。
2本の平行線がある場合に、三角定規を活用するとよりイメージしやすいです。
まず1本の直線を縦向きに描いてみてください。
このとき、真っすぐではなく、傾けて描いてもかまいません。
そして、三角定規の1辺と描いた直線をぴったりと合せて、三角定規の他の1辺を使って直線を引きます。
その後、三角定規を好みの位置までスライドさせて、同様にもう1辺描いてみてください。
そうすると、同じ角度の同位角が2つ出来上がります。
同位角ができることで、先述したように対頂角の関係で錯角ができるため、両者は同じ角度になるわけです。

錯角の4つのパターン

錯角には4パターンがありますが、位置関係で掴みにくい方もいるでしょう。
ここで錯角の4パターンについて解説しますので、位置関係を確認しておきましょう。
再度、確認すると、錯角は2本の平行線と交わる1本の直線において、向かいの位置関係です。
ここで、図で見たときの特徴を言うと、錯角はアルファベットの「Z」の形をしています。
錯角の位置関係の角を作るように一筆書きにすると「Z」と覚えると、錯角を見つけやすいでしょう。
問題によっては「Z」の向きが変わったり、つぶれた形に見えたりしますが、Z型になっているのが錯角です。

錯覚の証明問題を解いて見よう

ここからは錯角の証明問題をいくつか出題しますので、解いてみてください。

練習問題①

まずは次の3問に挑戦してみてください。

解説

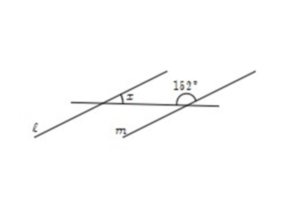
①角xの錯角は152°の角の左側になります。
よって、180°-152°＝28°が角xの大きさです。
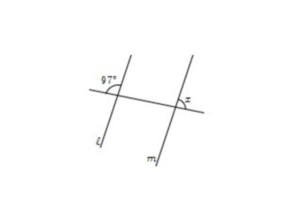
②角x、さらに97°の角で錯角は見つけられない（Z型を描けない）ので、97°の角で同位角を見つけます。
そうすると、角xの左側の角が97°になります。
よって、角xを求めるには、180°‐97°＝83°と計算します。
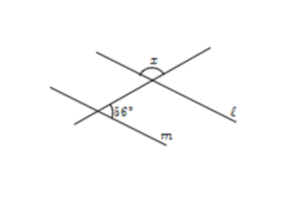
③角xの錯角は図で見つけられないので、56°の角で錯角を見つけます。
56°の錯角は角xの左側になります。
よって、角xは180°-56°＝124°です。

練習問題②

次は少しレベルを挙げて出題します。

解説

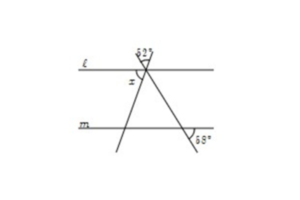
①角xの錯角は図中にできる三角形の左下の角になります。
さらに対頂角の関係から、三角形の頂角が52°、右下の角が58°です。
よって、三角形の内角の和（180°）より、角xは180°-52°-58°=70°となります。
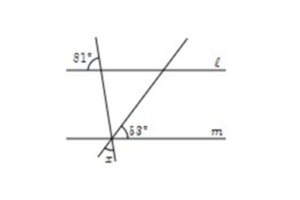
②53°の角の錯角が図中にできる三角形の左上の角であり53°。
81°の対頂角が、三角形の右上の角、角xの対頂角が頂角になります。
よって、三角形の内角の和（180°）より、角xは180°-53°-81°=46°となります

練習問題③

さらにレベルを挙げて出題します。

解説

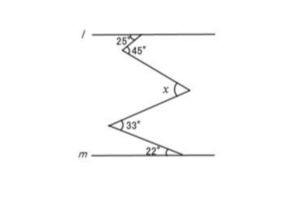
①45°角にlとmに平行な補助線を引きます。
そうすると、25°の角の錯角で上側が20°です。
さらに角xにも同様に補助線を引くことで、45°の角の下側（20°）と角xの上側が錯角で同じ角度になります。
また、33°の角にも同様の補助線を引いてみると下側が22°、上側が11°です。
この11°は補助線を引いた角xの下側と同じ大きさ。
つまり、角xは、20°＋11°＝31°です。
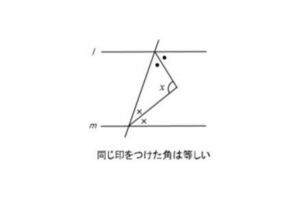
②2つの「●」を分けている直線を延長して直線ｍまで伸ばします。
そうすると、頂角が「●」、錯角により右下の角「●」、左下の角「×」が2つ分の三角形が出来上がります。
つまり、その三角形は「●」2つと「×」2つで180°の三角形になります。
2●＋2×＝180°、両辺を2で割って●＋×＝90°と計算できます。
ここで角ｘと●と×の3つの角でできる三角形に注目してください。
●と×は合せて90°ですから、角x＝180°-90°＝90°になります。

中学の数学は基礎力が大切

中学校の数学は基礎力が非常に大事です。
その理由や額主方法などを解説します。

中学数学でつまずくと高校数学ができない

中学数学は高校数学につながる内容となるため、つまずくと高校数学も理解しづらくなります。
例えば、今回、解説しているさまざまな角の位置関係や角度を求めたりすることは、高校数学の図形分野で当たり前にできることが前提です。
さらに高校数学では新たな定理が次々に登場しますので、中学数学の定理などを覚えきれていないと、高校数学はお手上げ状態になってしまうのです。
もちろん、図形分野以外も同様です。
中学3年生で学習する因数分解は高校数学でも頻繁に使い、さらに応用を履修します。
どの単元も高校数学の基礎となるため、その基礎力を身につけておく必要があります。

将来の選択肢が狭まる危険も

中学数学でつまずくと、将来の選択肢が狭まる危険があります。
中学校までであれば、数学が苦手でも他の科目でカバーして高校受験などをクリアできるかもしれません。
しかし、高校で文系と理系を選択する際に、数学が苦手な場合は、理系を選びにくいです。
また、基本的に理転といって、文系から理系に変更するのは難易度が高まります。
逆に文転で理系から文系に移るのはそこまで難しくありません。
文系を選ぶ人のほとんどは数学や理科が苦手という理由です。
しかし、苦手だからという理由だけで文系を選ぶと、いざ理系の大学を受験しようと思ってもなかなか難しくなり、選択肢も狭くなるのです。
将来的な選択肢を広げるためにも、数学に苦手意識を持たないように取り組むことが大事です。

とにかく基礎や定義を覚えることが重要

中学数学ではさまざまな定理や公式が登場します。
しかし、それらの定理や公式を丸暗記しようとすると大変であり、そこから苦手意識を持つ可能性もあります。
今回は対頂角や同位角、錯角が等しくなることを証明しました。
定理や公式が証明できれば、納得して覚えることができ、数学の理解力も高まります。
そのため、丸暗記ではなく、なぜそうなるのかも考えてみましょう。
そして、全単元に言えることは、基本を徹底することです。
基本問題を数多くこなすことで、定理や公式の使い方も身に付き、忘れにくくなります。
結果として、多少、数学が苦手でも平均点など、一定程度の点数が取れるようになります。

数学を学習するなら個別の会

数学を苦手にする人は少なくありません。
特に自分で解決できないことが増えやすい教科であり、自主学習も思うように進まないこともあるでしょう。
数学の学習に困っている場合は「個別の会」の授業を受けてみてください。
個別の会は、経験豊富なプロ講師が、1人ひとりも苦手分野を的確に把握し、分かりやすく解説します。
基礎からスタートしても大幅に偏差値がアップ、定期テストの得点も大きく向上させております。
各生徒に合わせたカリキュラムで、柔軟に指導しますので、この機会に個別の会のご利用をご検討ください。

まとめ

今回は、対頂角、同位角、錯角について、位置関係や等しくなる理由を解説しました。
また、レベル別にいくつかの練習問題もご紹介しましたので、日々の学習などにご利用ください。
数学は将来の選択肢にも影響する大事な教科であるため、できるだけ苦手意識を持たず、取り組むことが必要です。
基本を徹底して、苦手意識を払拭していきましょう。
また、数学の学習に困ったときは、個別の会にご相談ください。
1人ひとりに最適なカリキュラムの提案や、指導をいたします。